Everybody knows the definition of prime numbers. A number is a prime number when its only factors are 1 and the number itself. It’s common to hear people say that prime numbers are the building blocks of numbers. But how?
In simple terms: we can use multiplication to build any whole number from prime numbers alone.
We do this by multiplying the smallest whole numbers possible that can make up a number.
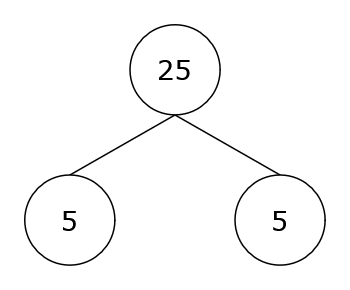
Let’s say we want to create the number 25. Extract the possible combinations of multiplication that build up this number.
Don’t be puzzled if you don’t understand this. We are trying to find the smallest factors that multiply to our goal number. There are multiple techniques to this. Below is how I do it.
Since 1 is not a prime number, we skip that one and start the multiplier with 2. Multiply 2 with an increasing multiplicand until we get exactly 25.
$$
2\times2 = 4\\
2\times3 = 6\\
2\times4 = 8\\
…\\
2\times13 = 26
$$
\(2\times13\) is greater than 25 so we have to increment the multiplier.
$$
3\times3 = 9\\
3\times4 = 12\\
3\times5 = 15\\
…\\
3\times9 = 27
$$
\(3\times9\) is greater than 25 so we have to increment the multiplier.
Keep repeating until we get exactly 25.
$$
4\times4 = 16\\
4\times5 = 20\\
4\times6 = 24\\
…\\
5\times5 = 25
$$
Finally! The number 25 is made up of \(5\times5\).
Next we’ll have to do the same for the number 5. Since we know that no number can multiply to 5 because 5 is a prime number, we can stop here.
You can see that all of the minutest numbers that make up 25 are all prime numbers. Isn’t this amazing?!
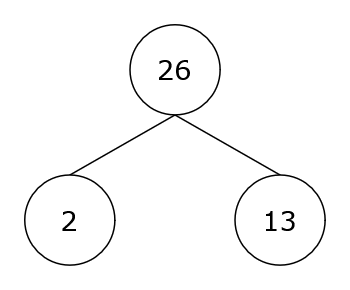
Let’s try again for the number 26. This time we get \(2\times13\)
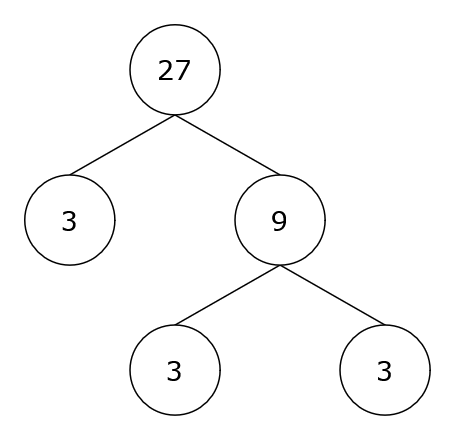
Let’s try again for the number 27. This time we first get \(3\times9\) but 9 can be extracted into \(3\times3\) so in the end we get \(3\times3\times3\).
I hope this post clears up your confusion and satisfies your curiosity how prime numbers are the building blocks of numbers.